자료구조
개요
정의
프로그램에서 저장하는 데이터에 대해 탐색, 삽입, 삭제 등 연산을 효율적으로 수행하기 위해 동일한 타입의 데이터 정리하여 저장한 구성체
분류
파일 : 같은 타입의 레코드들의 집합
기본적으로 저장된 레코드들이 어떻게 접근할 수 있게 하는지에 따라 크게 순차 방법, 인덱스 방법, 해싱 방법 등으로 나눌 수 있음.

리스트
▶ 선형 리스트 (Linear List)
- 선형 리스트의 대표적인 구조 "배열(Array)"
- 가장 간단하고 접근 속도가 빠름
- 동일 타입의 데이터들이 연속적인 메모리 공간 (기억 장소)에 할당되어 각각의 데이터들이 하나의 공간에 저장되는 기본적인 자료구조
- 자료의 삽입, 삭제 시 저장 공간의 이동이 필요함 - 번거로움
- 최초에 배열 크기 예측해서 결정해야 하므로 빈 공간이 존재할 수 있음

▶ 연결 리스트 (Linked List)
- 자료들을 선형 리스트처럼 연속으로 배열시키지 않고, 임의의 기억 공간에 기억 시키되 각 노드 포인터를 이용하여 서로 연결함
- 포인터 사용으로 기억 공간이 연속적으로 놓여있지 않아도 저장이 가능하고 노드의 삽입, 삭제가 용이함
- 노드가 추가되면 포인터도 추가로 필요하기 때문에 기억 공간을 더 필요로 함
- 데이터 접근 시 포인터를 찾는 시간이 필요하므로 순차 리스트에 비해 느림
- 데이터를 DB에 저장하기 위한 데이터 구조로서, 물리 데이터 저장소와는 별개로 사용자 혹은 개발자가 이해하기 쉬운 논리적인 구조로 추상화하여 제공함

스택 (Stack)
- 한쪽 끝에서만 자료 삽입, 삭제 가능한 LIFO (Last In First Out - 후입선출) 형식의 자료구조
- 컴파일러의 괄호 짝 맞추기, 미로 찾기, 트리의 노드 방문, 그래프 깊이우선탐색, 인터럽트 수행 시 복귀 주소 저장, 수식 연산 등에서 사용됨
- Push : 데이터 삽입 연산
- Pop : 데이터 삭제 연산
- Top : 가장 위에 있는 데이터를 가리키는 변수

▶ 수식 표기법

1. 중위 표기법 (Infix Notation)
- 피연산자1, 연산자, 피연산자2 순서로 수식 표현하는 표기법
- 연산자가 피연산자들 사이에 위치

2. 전위 표기법 (Prefix Notation)
- 연산자, 피연산자1, 피연산자2의 순서로 수식 표현하는 표기법
- 연산자가 가장 앞에 위치

- 괄호 사용하여 변환 방법
- 연산자의 우선 순위에 맞게 괄호 적용
- ((A+B)/(C-D))
- 괄호 안에 있는 연산자를 괄호 앞으로 배치 후 괄호 제거
- (+(AB)/-(CD)) → (+AB/-CD) → /+AB-CD
- 연산자의 우선 순위에 맞게 괄호 적용
3. 후위 표기법 (Postfix Notation)
- 피연산자1, 피연산자2, 연산자 순서로 수식 표현하는 표기법
- 연산자가 가장 끝에 위치
- 컴파일러가 주로 샤용
- 괄호가 없어도 우선순위 반영되어 있음

- 괄호 사용하여 변환 방법
- 연산자의 우선 순위에 맞게 괄호 적용
- ((A+B)/(C-D))
- 괄호 안에 있는 연산자를 괄호 뒤로 배치 후 괄호 제거
- ((AB)+/(CD)-) → (AB+/CD-) → AB+CD-/
- 연산자의 우선 순위에 맞게 괄호 적용
- 스택 사용하여 변환 방법
- [규칙 1] 피연산자는 스택에 저장하지 않고 바로 출력
- [규칙 2] 왼쪽 괄호면 push
- [규칙 3] *, / 연산자면 push
- [규칙 4-1] + - 연산자일 때 바로 다음이 피연산자이면 push
- [규칙 4-2] + - 연산자일 때 바로 다음이 왼쪽 괄호이면 스택 끝까지 pop 후 연산자 및 왼쪽 괄호 push
- [규칙 5] 오른쪽 괄호이면 왼쪽 괄호가 나올 때까지 pop
- stack [ ] (A+B)/(C-D) print [ ]
- stack [ ( ] A+B)/(C-D) print [ ] [규칙 2]
- stack [ ( ] +B)/(C-D) print [ A ] [규칙 1]
- stack [ ( + ] B)/(C-D) print [ A ] [규칙 4-1]
- stack [ ( + ] )/(C-D) print [ A B ] [규칙 1]
- stack [ ] /(C-D) print [ A B + ] [규칙 5]
- stack [ / ] (C-D) print [ A B + ] [규칙 3]
- stack [ / ( ] C-D) print [ A B + ] [규칙 2]
- stack [ / ( ] -D) print [ A B + C ] [규칙 1]
- stack [ / ( - ] D) print [ A B + C ] [규칙 4-1]
- stack [ / ( - ] ) print [ A B + C D ] [규칙 1]
- stack [ ] print [ A B + C D - / ] [규칙 1]
큐 (Queue)
- 삽입과 삭제가 양 끝에서 각각 수행되는 FIFO (First In First Out - 선입선출) 형식의 자료구조
- Front Pointer : 삭제 작업 시 사용되는 곳
- Rear Pointer : 삽입 작업 시 사용되는 곳
- enQueue : 데이터 삽입 연산
- deQueue : 데이터 삭제 연산

데크 (Deque, Double Queue)
- 양쪽 끝에서 삽입과 삭제를 허용하는 자료구조 ( 데크 = 스택 + 큐 )
- 스택과 큐를 동시에 구현하는 데 사용됨
- 스크롤 (Scroll), 문서 편집기 등의 Undo (취소) 연산, 웹 브라우저 방문 기록 등에서 사용됨
- 웹 브라우저 방문 기록의 경우, 방문 주소는 앞에 삽입하고 일정 수의 주소들이 삽입되면 뒤에서 삭제가 수행되는 형태로 처리

트리 (Tree)
- 탐색 연산이 순차적으로 수행되는 배열이나 연결 리스트의 단점을 보완한 계층적 (Hierarchical) 자료 구조
- 조직이나 기관의 계층 구조, 컴퓨터 OS 파일 시스템, 자바 클래스 계층 구조 등에서 사용됨
- 인덱스 조작하는 방법으로 가장 많이 사용되는 구조
- 트리 = 노드 (Node) + 링크 (Link)

- 루트노드 (Root Node) : 부모가 없는 노드. 트리는 하나의 루트노드만 가질 수 있음 ▷ A
- 단말노드 (leaf Node) : 자식이 없는 노드 ▷ D, E, F
- 내부노드 (Internal Node) : 루트노드와 단말노드가 아닌 노드 ▷ B, C
- 링크 (Link) : 노드를 연결하는 선 (= Edge, Branch)
- 형제 (Sibling) : 같은 부모를 가지는 노드 ▷ [B, C] 또는 [D, E]
- 노드의 크기 (Size) : 자신을 포함한 모든 자손 노드의 개수 ▷ B의 크기 : 3 (B,D,E), C의 크기 : 2 (C, F)
- 노드의 깊이 (Depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선(링크)의 수 ▷ D의 깊이 : 2, C의 깊이 : 1
- 노드의 레벨 (Level) : 트리의 특정 깊이를 가지는 노드의 집합 ▷ A의 레벨 : 1, B의 레벨 : 2
- 노드의 차수 (Degree) : 특정 노드의 자식 수 또는 간선(링크)의 수 ▷ A의 차수 : 2 (B, C), C의 차수 : 1 (F)
- 트리의 차수 (Degree of Tree) : 트리의 최대 차수. 트리에서 자식을 가장 많이 가지는 노드의 차수 ▷ B의 차수 : 2
- 트리의 높이 (Height) : 루트노드에서 가장 깊이 있는 노드의 깊이 ▷ D의 깊이 : 2
▶ 트리의 기본적인 성질
- 노드가 N개인 트리는 항상 N-1개의 링크를 가짐
- 루트노드에서 특정 노드로 가는 경로는 유일함
- 임이의 두 노드 간의 경로도 유일함 (같은 노드를 두 번 이상 방문하지 않는다는 조건)
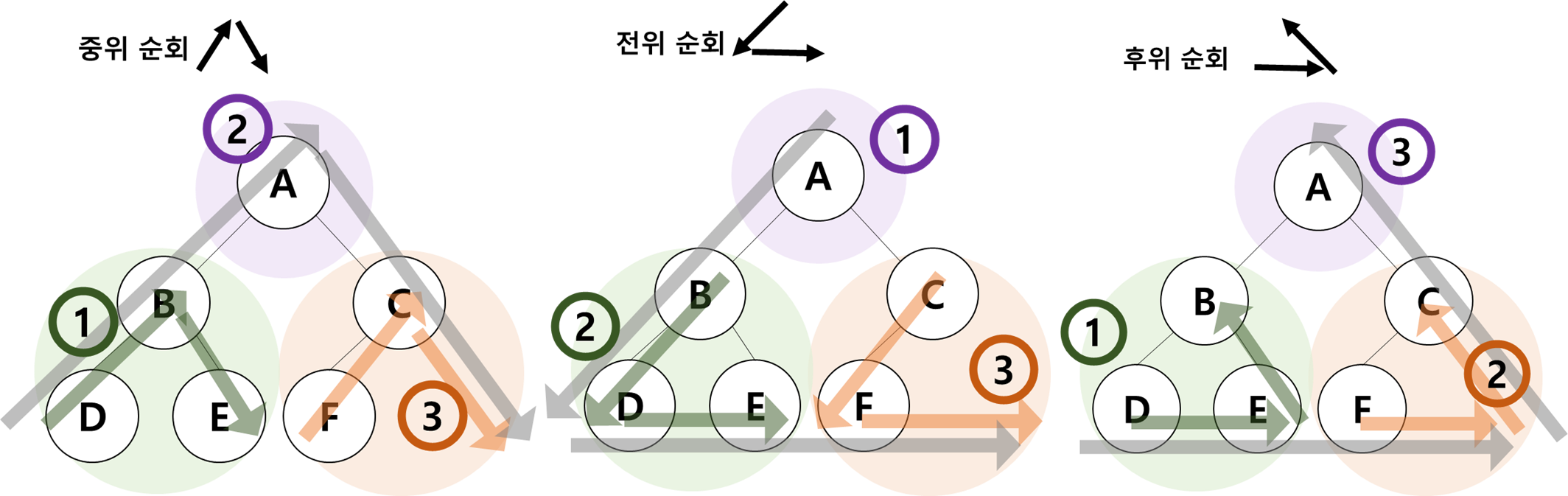
▶ 트리의 순회 (Traversal) 방법
중위 순회 (Inorder Traversal)
- 순회 방법 : 왼쪽노드 → 중간노드→ 오른쪽노드
- DBE A FC
전위 순회 (Preorder Traversal)
- 순회 방법 : 중간노드 → 왼쪽노드 → 오른쪽노드
- A BDE CF
후위 순회 (Postorder Traversal)
- 순회 방법 : 왼쪽노드 → 오른쪽노드 → 중간노드
- DEB FC A
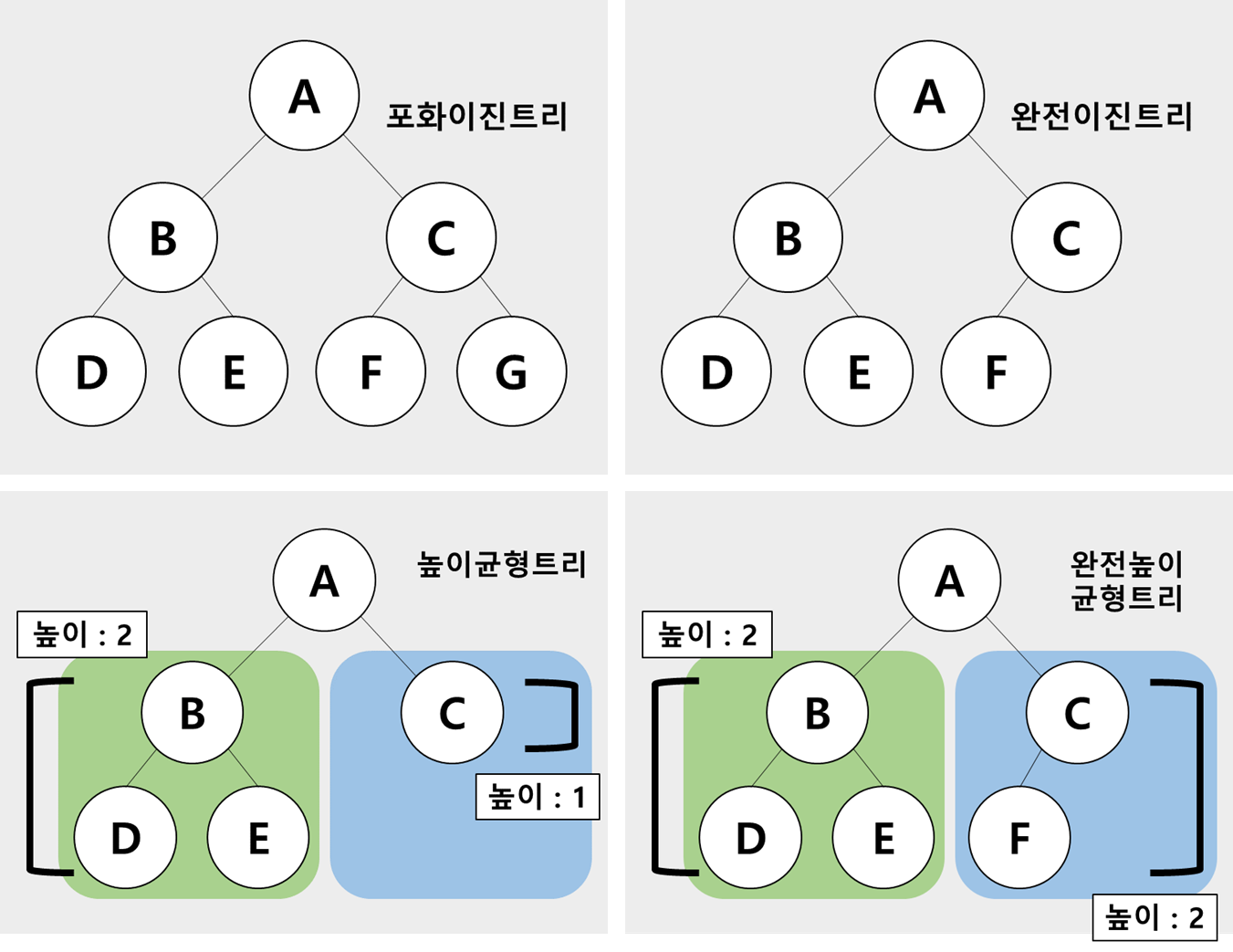
이진 트리 (Binary Tree)
- 한 노드가 최대 2개의 자식노드를 가지는 트리
- 높이가 h인 포화 이진 트리는 2^h - 1개의 노드를 가짐
- 노드가 N인 포화 혹은 완전 이진 트리의 높이는 O(log2 N)
- 노드가 N개인 이진 트리 높이는 최악의 경우 O(N)이 될 수 있음
- 포화 이진 트리 (Full Binary Tree) : 트리의 각 레벨에 노드가 다 차있는 이진 트리
- 완전 이진 트리 (Complete Binary Tree) : 잎 노드들이 트리의 왼쪽부터 차곡차곡 채워진 트리
- 높이 균형 트리 (Height Balanced Tree) : 루트노드를 기준으로 왼쪽 트리와 오른쪽 트리의 높이가 1 이상 나지 않는 트리
- 완전 높이 균형 트리 (Complete Height Balanced Tree) : 루트노드를 기준으로 왼쪽 트리와 오른쪽 트리의 높이가 같은 트리
그래프 (Graph)
- 특정 집단 내 각각의 단위 정보를 링크로 연결하여 구조화시킨 자료구조
- 노드와 노드를 연결하는 간선을 하나로 모아 놓은 자료구조
- 노드 ( N ), 간선 ( E ), 정점 ( V ), 그래프 ( G ) = (V, E)
- 차수 (Degree) : 특정 정점에 연결되어 있는 변의 개수, 또는 특정 정점에 인접한 정점의 수
- 사이클 (Cycle) : 처음과 마지막 정점이 같은 단순 경로.
1. 방향 그래프 (Directed Graph)
- n개의 정점이 있는 경우 간선의 수는 n(n-1)
2. 무방향 그래프 (Undirected Graph)
- n개의 정점이 있는 경우 간선의 수는 n(n-1)/2

3. 완전 그래프
- 그래프에서 간선의 수가 최대인 그래프
4. 부분 그래프
- 그래프G의 일부분인 그래프G1. V(G) ⊆ V(G1) 이고, E(G1) ⊆ E(G)로 표현
5. 신장 트리 (Spanning Tree)
- 그래프의 모든 정점들을 사이클 없이 연결하는 부분 그래프

▶ 그래프 순회 방법
1. 깊이 우선 탐색 (DFS)
- Stack 이용. 루트 또는 임의 노드에서 다음 노드로 넘어가기 전 해당 분기를 완벽하게 탐색하는 방법
2. 너비 우선 탐색 (BFS)
- Queue 이용. 루트 또는 임의 노드에서 인접한 노드를 모두 탐색하는 방법

320x100
'정보처리기사 > 필기' 카테고리의 다른 글
| [정보처리기사] Part02-03. 데이터조작 프로시저 최적화 (34) | 2023.01.08 |
|---|---|
| [정보처리기사] Part02-02. 데이터조작 프로시저 작성 (7) | 2023.01.08 |
| [정보처리기사] Part02-03-2. 제품 소프트웨어 메뉴얼 작성 (0) | 2022.07.15 |
| [정보처리기사] Part02-03-1. 제품 소프트웨어 패키징 (1) | 2022.07.15 |
| [정보처리기사] Part02-05-3. 인터페이스 구현 검증 (0) | 2022.02.25 |



댓글